La divergencia es un concepto fundamental que encuentra su aplicación en diversos campos científicos y matemáticos. En esencia, designa la situación en la que elementos, ya sean físicos, económicos o de opinión, se alejan unos de otros en lugar de reunirse.
En el ámbito del análisis vectorial, la divergencia es un operador que permite medir cómo se comporta un campo de vectores en relación con un punto dado. Más precisamente, cuantifica la variación de volumen de una región bajo el efecto de un campo de flujo. En otras palabras, la divergencia ilustra cómo un campo de vectores puede crear o aniquilar volumen en el espacio circundante, aportando así una visión clara de la dinámica de los fluidos y los campos electromagnéticos.
La significación física de la divergencia se explica a menudo a través de ejemplos provenientes del electromagnetismo o de la mecánica de fluidos. Por ejemplo, en el contexto de un fluido en movimiento, la divergencia puede indicar si el fluido se expande, se comprime o se mantiene constante en un punto específico. Una divergencia positiva en un punto podría significar que el volumen aumenta, mientras que una divergencia negativa indicaría una compresión.
En lo que respecta al cálculo vectorial, la comprensión de la divergencia ayuda a visualizar cómo interactúan los vectores en un punto fijo del espacio. Esto es particularmente relevante en finanzas, donde se observan movimientos de precios a través de indicadores técnicos. El análisis de estos movimientos puede permitir decisiones informadas en materia de trading.
Desde el punto de vista económico, la divergencia toma otra forma, especialmente cuando se habla de convergencia y divergencia de las medias móviles. La convergencia se refiere a un acercamiento entre estas medias, mientras que la divergencia describe una situación en la que se alejan una de la otra, indicando potencialmente una inestabilidad en las tendencias del mercado.
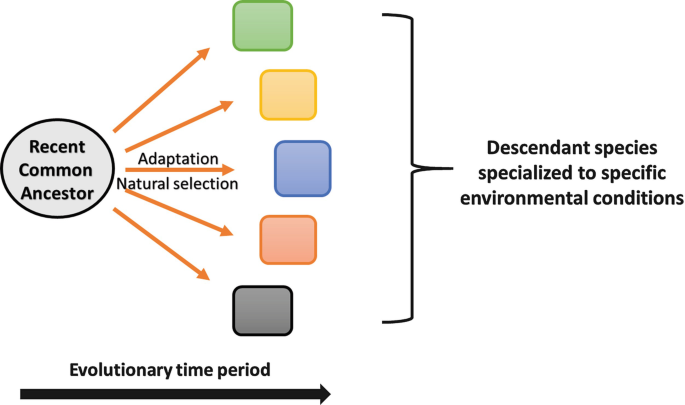
En biología, también se puede observar la divergencia genética, que se manifiesta cuando diferentes poblaciones de una misma especie comienzan a acumular diferencias a lo largo del tiempo. Esta divergencia puede favorecer adaptaciones ecológicas variadas y eventualmente llevar a especiaciones distintas. Cuanta más divergencia hay dentro de las poblaciones, más pueden estos grupos evolucionar hacia nichos ecológicos únicos.
Las divergencias de opinión constituyen un aspecto mayor en las interacciones sociales y la toma de decisiones. Este fenómeno puede generar malentendidos, desacuerdos o debates enriquecedores, dependiendo de cómo se gestione. Es vital reconocer que la divergencia no significa necesariamente un desacuerdo infranqueable, sino que también puede ser la oportunidad para una discusión constructiva.
Finalmente, en el ámbito de las ciencias, la divergencia también se menciona en el contexto de teoremas matemáticos, ayudando a establecer relaciones entre los diferentes tipos de derivadas y operadores. Estos teoremas desempeñan un papel crucial en la modelización y comprensión de sistemas complejos y dinámicos.
