The divergence is a fundamental concept that finds its application in various scientific and mathematical fields. Essentially, it refers to a situation where elements, whether physical, economic, or opinion-based, move away from each other instead of coming together.
In the field of vector analysis, divergence is an operator that allows us to measure how a vector field behaves with respect to a given point. More specifically, it quantifies the change in volume of a region under the influence of a flux field. In other words, divergence illustrates how a vector field can create or annihilate volume in the surrounding space, thus providing a clear view of fluid dynamics and electromagnetic fields.
The physical meaning of divergence is often explained through examples from electromagnetism or fluid mechanics. For instance, in the context of a moving fluid, divergence can indicate whether the fluid is expanding, compressing, or remaining constant at a specific point. Positive divergence at a point could signify that the volume is increasing, while negative divergence would indicate compression.
With regard to vector calculus, understanding divergence helps to visualize how vectors interact at a fixed point in space. This is particularly relevant in finance, where price movements are observed through technical indicators. Analyzing these movements can lead to informed decisions in trading.
From an economic standpoint, divergence takes another form, especially when discussing convergence and divergence of moving averages. Convergence refers to a coming together of these averages, while divergence describes a situation where they move away from each other, potentially indicating instability in market trends.
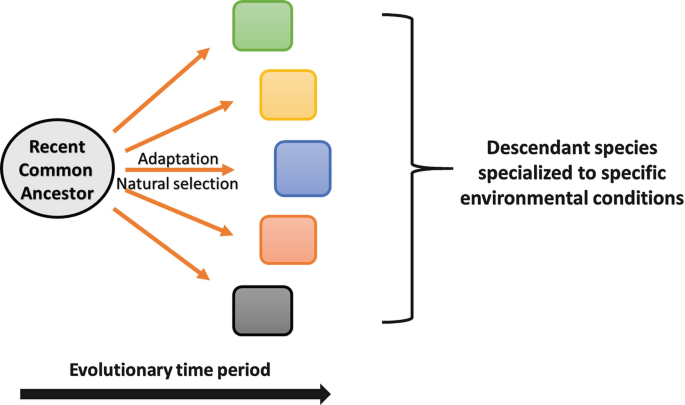
In biology, we can also observe genetic divergence, which occurs when different populations of the same species begin to accumulate differences over time. This divergence can promote various ecological adaptations and eventually lead to distinct speciations. The greater the divergence within populations, the more these groups can evolve toward unique ecological niches.
Divergences of opinion constitute a major aspect of social interactions and decision-making. This phenomenon can lead to misunderstandings, disagreements, or enriching debates, depending on how it is managed. It is vital to recognize that divergence does not necessarily mean an unbridgeable disagreement, but can also be an opportunity for constructive discussion.
Finally, in the field of sciences, divergence is also mentioned in the context of mathematical theorems, helping to establish relationships between different types of derivatives and operators. These theorems play a crucial role in modeling and understanding complex and dynamic systems.
